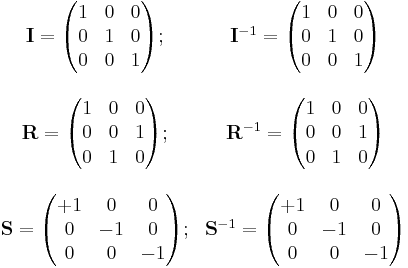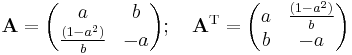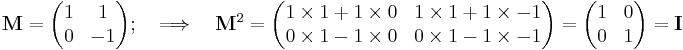Involutory matrix

In mathematics, an involutory matrix is a matrix that is its own inverse. That is, matrix A is an involution if and only if A2 = I. One of the three classes of elementary matrix is involutory, namely the row-interchange elementary matrix. A special case of another class of elementary matrix, that which represents multiplication of a row or column by −1, is also involutory; it is in fact a trivial example of a signature matrix, all of which are involutory.

Involutory matrices are all square roots of the identity matrix. This is simply a consequence of the fact that any nonsingular matrix multiplied by its inverse is the identity. If A is an n × n matrix, then A is involutory if and only if ½(A + I) is idempotent.

An involutory matrix which is also symmetric is an orthogonal matrix, and thus represents an isometry (a linear transformation which preserves Euclidean distance). A reflection matrix is an example of an involutory matrix.

Clearly, any block-diagonal matrices constructed from involutory matrices will also be involutory, as a consequence of the linear independence of the blocks.

Examples

Some simple examples of involutory matrices are shown below.

\begin{array}{cc} \mathbf{I}=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} ; & \mathbf{I}^{-1}=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ \\ \mathbf{R}=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} ; & \mathbf{R}^{-1}=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} \\ \\ \mathbf{S}=\begin{pmatrix} %2B1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{pmatrix} ; & \mathbf{S}^{-1}=\begin{pmatrix} %2B1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{pmatrix} \\ \end{array}

where

I is the identity matrix (which is trivially involutory);
R is a matrix with a pair of interchanged rows;
S is a signature matrix.

An interesting general condition exists, for 2 × 2 matrices, where any matrix that may be written in the form A or AT below:

\mathbf{A}=\begin{pmatrix} a & b \\ \frac{(1-a^2)}{b} & -a \end{pmatrix};\quad \mathbf{A}^\mathrm{T}=\begin{pmatrix} a & \frac{(1-a^2)}{b} \\ b & -a \end{pmatrix}

is involutory.

For example, for a matrix M of this form, where we set a = 1, b = 1, we have

\mathbf{M}=\begin{pmatrix} 1 & 1 \\ 0 & -1 \end{pmatrix};\quad\Longrightarrow\quad \mathbf{M}^2=\begin{pmatrix} 1\times 1%2B1\times 0 & 1\times 1%2B1\times -1 \\ 0\times 1-1\times 0 & 0\times 1-1\times -1 \end{pmatrix} =\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \mathbf{I}

See also